Overfitting and Underfitting in Machine Learning

Karen Tao, UX Researcher
May 27, 2020

Photo by Isaac Smith

As we build machine learning models that learn from training data with the goal to generalize to new unseen data, one of the most common errors is overfitting. We will discuss overfitting and underfitting today, and lay a foundation for understanding the bias-variance tradeoff in a future post.

Overfitting happens when the model captures the noise along with the underlying pattern. The model may do well with our training data, but it cannot be reliably generalized to new unseen data. The model is picking up random fluctuations or irrelevant information in the training data. For example, you want to build a model that can classify whether a picture contains a dog or a cat, one of the classic homework problems in classifications. You excitedly take many pictures of your sweet golden retriever and your adorable bombay. After working on your model and inputting these pictures, the model now does exceptionally well when it sees a picture of the pup or the kitty. You decide to test the model on some unseen pictures of your sister’s chocolate lab and American bobtail, and the accuracy drops significantly. Your model may be overfitting, as it picked up fur color as an important feature when distinguishing cats from dogs. It performed well with your training data, your own pets, and its performance suffered when given unseen test data, your sister’s pets.

On the other hand, models could suffer from underfitting. Underfitting happens when a model is not complex enough. This makes it inflexible in learning from the dataset. If the model performs poorly on the training data, it is possible that it is underfitting. The model is not capturing the underlying pattern. Below is an illustration of what overfitting and underfitting would look like.

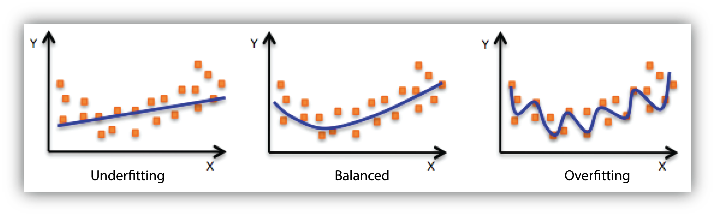
The data points from the training set are in orange, and the blue line represents the model. The overfitted model discovers the trend and is able to accurately “fit” all data points in the training data, but it is now too specific. It has learned the training data too well and its prediction on new data would be unreliable. The underfitted model detects a general trend in the data, but it is not specific enough to capture the underlying pattern. Its performance would be poor for both training or new data.

Overfitting tends to be associated with low bias and high variance, and underfitting tends to be associated with high bias and low variance. As demonstrated, overfitted models are flexible, and they allow for higher variation within the data. Underfitted models are too simple and do not learn from the training data well. In my next blog, we will formally introduce bias error and variance error, and dive deeper into the bias-variance trade-off.