An introduction to cross-validation
Karen Tao, UX Researcher
October 7, 2020

Photo by Caleb Woods
Recall from a previous post, a training set in machine learning is a subset of our data used to train our machine learning model. After the model is trained, we use the test set, data previously unknown to the model to evaluate the performance of our model. Cross-validation is a resampling technique that builds upon that idea. It is such a fundamental concept in statistics that the Stack Exchange community for statistics, equivalent for stackoverflow for programmers, is named “Cross Validated.”
In cross-validation, our modeling process is evaluated on different subsets of the data to get multiple measures of model performance. One of the most common approaches is k-fold cross-validation. After randomly shuffling the dataset, we separate the dataset into k subsets, where k is a parameter for the number of subsets we split our data into.
For example, let’s say we are training a model to predict whether a student stays in the Utah workforce after obtaining a post-secondary degree. If our dataset consists of 10,000 students, and we choose k to be 5, we would perform 5-fold cross-validation. We would evenly split the 10,000 students into 5 groups after shuffling them. Each group would have 2,000 students. We would first train our model on groups 1-4, using group 5 as the test set and record the test error for group 5. Group 5 in this instance is called the holdout sample. In our second iteration, we would train the model on groups 1, 2, 3, 5, using group 4 as the test set and record the test error for group 4. Group 4 is the holdout sample in this round. We would keep repeating this procedure until we are done training the model on groups 2-5, using group 1 as the test set and record the test error for group 1. Finally, we aggregate the test errors from each round, usually taking the average, to determine model performance. Below is a visual representation that illustrates this process.
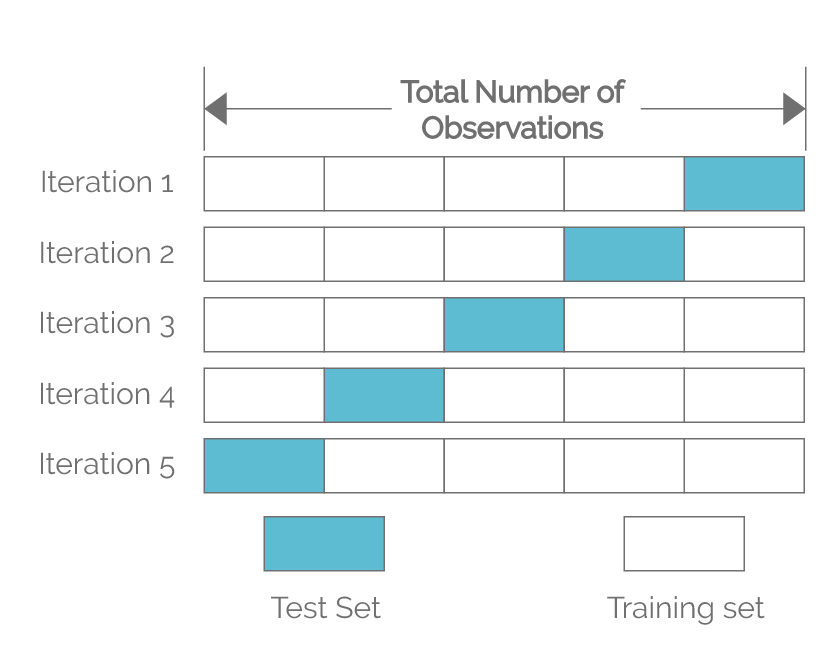
We see that the each of the 5 groups takes turns crossing over in each iteration. As a result, each data point, or student in our example, would be validated against once, and would be used as training data 4 times, or k-1 times. The computational cost for our 5-fold cross-validation would be 5 times what it would be if we had only trained the model once and evaluated once because we are essentially training and evaluating our model k times during cross-validation. Typically, k=10 is common in machine learning as it tends to provide good trade-off of low computational cost and low bias in estimating model performance.
Another variation of cross-validation is setting the parameter k to the sample size n. In our example, this means k = 10,000. This is called leave-one-out cross-validation (LOOCV). In LOOCV, each student is given a chance to be the only data point in the holdout. The model gets evaluated using each student individually instead of a group of students. However, the computational cost for LOOCV would be high because we would be training and evaluating the model n times. Depending on the size of the dataset you are working with, it could be an art to determine the best value to set your k to. Here is an article that takes a closer look at how to choose k.
I hope this post provides the theoretical understanding of cross-validation. If you’d like to get some hands-on experience, the sklearn library for python has a class named KFold that can get you started. Happy coding!