Instrumental Variables and Endogeneity Part 1: Theory

Ari Fenn, Researcher
August 4, 2021

Our research at the UDRC is often about the relationship between education and a wide variety of labor market outcomes. We have published several reports that use higher wages associated with post-secondary education as a mediator for downstream outcomes of interest.¹ Unfortunately, many studies cannot establish a causal effect of education on wages due to the existence of endogeneity.

In this blog post, I will first define endogeneity. Then I will introduce the standard technique to correct the endogeneity problem — Instrumental Variables (IV) estimation. Finally, I will give two tractable examples of this method.

In a subsequent blog post, I will show how to execute the technique in R and review some statistical tests for the appropriateness of the method.

Endogeneity occurs when one of the explanatory variables in a regression model is correlated with the error term. It can occur due to unobserved heterogeneity or an omitted variable which causes the estimated regression coefficients to be inconsistent. I present a technical demonstration at the end of this blog post for those who are interested.

In the relationship between education and wages, years of education may be correlated with an unobserved heterogeneity; the correlation could be with individual productivity, determination, ability, or similar reasons that someone may obtain post-secondary education and have higher wages. Thus, IV estimation is appropriate when estimating which consistent regression coefficients to use in the presence of unobserved heterogeneity.

An instrumental variable or instrument is a variable that is correlated with the endogenous explanatory variable, such as years of schooling, but not the error term or the unobserved variable. When an appropriate exogenous variable or variables have been identified, IV estimation is a simple process. A first stage estimation regresses the exogenous explanatory variables of interest and the endogenous variable instrument. Predicted values of the endogenous variable are then used to estimate the effect on the outcome of interest.

If a proper instrument was identified, the predicted values of the endogenous variable should no longer be correlated with the error term. Thus, a useful instrument solves the problem of endogeneity. Computationally, an IV estimate is easy. The complicated part is figuring out an appropriate instrument.

Choosing an instrument is not always a straightforward process. A correct instrument is both correlated with the endogenous variable and uncorrelated with the error term. In the case of the returns to education, there have been many papers that use different instruments. Choosing an instrument takes a deep understanding of why there is endogeneity. Below I present two examples of an IV approach on the returns to education.

In a seminal paper, Angrist & Krueger (1991) estimate the effects of years of schooling on wages. This paper is a classic example of endogeneity; the authors were unable to control for individual ability or drive but did have data on the month of birth. The authors explained that schooling was only compulsory up to the age of 16 and that students in the same grade can start with an eleven-month age gap. Students born later in the year would not be able to stop attending school before finishing out that school year, while those born earlier could drop out of school and begin earning wages full-time. This age difference upon school entrance was used in their analysis, where the quarter of birth was used as an educational instrument. There was no reason that quarter of birth should be related to individual ability, but it did determine when school no longer became compulsory (Angrist & Krueger, 1991).

A study estimating the effects of post-secondary education on welfare recipients (London 2006) uses instrumental variables for both post-secondary attendance and post-secondary graduation. Instrumental variables are needed in this study since the choice to attend a post-secondary institution may be determined by individual ability, motivation, and family expectations. Therefore, the instrument for parental expectations – the highest level of education for the mother - was included in the first stage estimation. In addition, the author uses percentile rank on a standardized test as an instrument for ability. Furthermore, London (2006) uses the number of two- and four-year institutions, post-secondary enrollment for the county of residence, and state-level average tuition cost as instruments for norms that may drive a student to enroll in a post-secondary institution.

It is worth noting that the number of post-secondary institutions in the county of residence as a measure of access is confirmed as a reasonable measure with forthcoming research from the UDRC. Furthermore, an additional instrument in the estimation of post-secondary graduation is the receipt of student loans; student loans help a student in financial need potentially graduate but are not based on an individual’s ability. Merit-based financial aid is based on ability, however, which will be endogenous (London, 2006).

These examples demonstrate instruments suited to account for the endogeneity inherent in many econometric models. These allow for a causal interpretation of the results of the regression estimates of the returns to education. While these instruments are concise and, after explanation, it is not always straightforward to determine an appropriate instrument. There are statistical tests that I will cover in a subsequent post. Before formal tests of an instrument, a compelling story about why any instrument should be correlated with an endogenous variable and not correlated with the error term is needed. To find an appropriate instrument, a researcher must start with a strong knowledge of both the subject of research and the data.

Technical Demonstration

From a standard linear regression model:

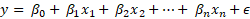
In the presence of endogeneity for explanatory variables but for the n^th explanatory variable Cov()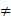0.

The instrument is a variable, z, that is uncorrelated with ϵ (the error term) but is correlated with the endogenous explanatory variable 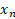. The simplest IV technique is a two-stage least squares with a first stage estimation equation:

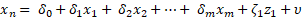
In the first equation, all of the exogenous variables and the instrument estimate the endogenous variable, 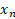. In the second stage, the estimated values of the endogenous variable, are included in the estimation of the outcome of interest:

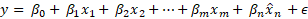
The predicted values of the endogenous variable will no longer be correlated with the error term, and a proper instrument solves the problem of endogeneity.