Skiing this weekend? A decision tree approach
Karen Tao, Researcher
November 3, 2021

A Decision Tree is a type of supervised machine learning. It is commonly visualized as a tree drawn upside down with its root at the top and leaves at the bottom. Data from the root are continuously split depending on whether they meet a condition. The main parts of a tree include decision nodes, tree branches, and leaves. The leaves are the labels or final outcomes that we are trying to predict. The tree branches or edges direct the data from the root to the leaves, while the decision nodes are where the data get split. We can think of the leaves as the labels or targets in supervised machine learning. Each internal node represents a test on an attribute. The edges act as the responses to the test on that attribute. Decision trees classify the data by sorting them down from the root to a leaf node, with the leaf node providing the classification.
For example, we are trying to predict whether we will go skiing this weekend. One of the first decision nodes may be whether we have enough snow in the mountains. If there is not enough snow, we are not likely to ski. The leaf, or outcome, would be a "no" label. Let's say we do have enough snow; we may proceed down the tree branch, or edge, of "enough snow" to our second decision node, which may be "do we have prior commitments." Answering "yes" to prior commitments may take us to a final outcome of "no" to skiing. Answering "no" to prior commitments may take us to a potential final outcome of "yes" to skiing or down the branch to another decision node where we will answer another yes/no question to split further.
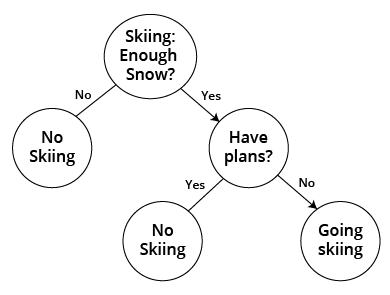
Decision trees can be used for classification and regression machine learning models. From our oversimplified binary example, you can see that the deeper the tree, the more nodes or complex the rules, and the model is fitter. Growing the tree requires the model to learn which attributes or features are more important and when to stop growing the branches. The algorithm is typically a greedy algorithm that grows the tree from the root to the leaves or top-down. At each node split, the algorithm selects the attribute that best classifies the local training data. This process continues down the tree until a leaf or label is reached.
Connecting back to our ski prediction example, our input data for the model includes 100 days of data with features such as snow accumulation, prior commitment, football Sunday, health status, and whether Taylor Swift released a new album that week. The labels yes/no to skiing are also included in our 100 days of test data. As the tree begins at the root, it asks questions about each of the features, snow/prior plans/football/healthy/new music, and determines which of these features best separates the 100 days of data. Once the first node, the most important feature, is selected, the model repeats a similar process to find the next most important attribute down each branch. The algorithm terminates when all features are examined or when the algorithm learns that the remaining features have no effect on predicting the target variable. In our example, our model may learn that Taylor Swift's new albums have no impact on ski decisions and will not use that feature as a node in our decision tree.
One of the advantages of decision trees is that we can see which features the model deems important. For example, imagine you have a dataset with 500 attributes, and you would like to know which of these attributes are important to the outcome variable. Decision trees are great tools to use. What we mean by "attributes important to the outcome" is measured by how well the attributes separate the data.
In information theory, a metric called entropy measures the level of impurity. For our simple binary example, entropy ranges between 0 and 1, with a higher value indicating higher impurity. Impurity happens when the model attribute does a terrible job separating the two different outcomes to our skiing example. For example, the question "do we have enough snow?" can probably do a better job at determining whether we go skiing than the question "did Taylor Swift release a new album?" Thus, impurity for the question regarding snow accumulation would be lower than the question about new music, and therefore entropy for the snow accumulation node would be lower.
From here, the model can calculate information gain, a metric that measures the reduction in impurity in the labels given additional information about a new feature. In our example, this could be calculating the reduction of uncertainty about skiing, given further information regarding our health. It's reasonable to stay home to nurse a sprained ankle even when we are 20 minutes away from the best snow on earth. The better our prediction about skiing, the purer the labels with information about health status, the greater the reduction in uncertainty, the more information is gained about skiing from health status and therefore higher importance of health. For those who learn best by studying mathematical formulas, check out this useful slide presentation.
Finally, careful readers may have noticed crucial faults in our ski prediction example. We only collected 100 days of data. If these were 100 days from the summer, the outcome would have been "no" to skiing for all 100 days. On the other hand, if we collected data from a ski patrol employee in the winter, the outcome would likely have been "yes" to skiing for all 100 days. The data scientist plays a key role in determining whether the data we collect is sufficient and relevant to the outcome we wish to predict. In addition to season and occupation, age and amount of disposable income may also affect one's skiing choices. Data scientists are critical in selecting the algorithms, building a model, and interpreting the results. Now put on your data scientist hat and get your hands dirty with implementing a decision tree in python.